Area of a Square

Lesson Objective

In this lesson, we will learn about the area of a square.

Study Tips

Tip #1

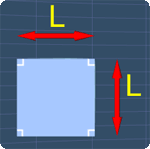
A square has four right angles and all the sides of a square have the same length.

Now, if the length of each side is L, the area, A of the square will be:

A = L²

The math video below will give more explanations on this. Also, we will see some examples on how to use the formula.

Math Video

Lesson Video

Sponsored Links

Math Video Transcript

00:00:03.180
In this lesson, we will learn about the area of a square.

00:00:08.180
Consider this square. All the sides of this square have the same length, L.

00:00:16.050
Now, we can get the area of this square, A, by multiplying both of these length L together.

00:00:23.130
With this, we get the area, A, equals to L multiply by L. This gives L square.

00:00:31.230
Note that, we also must include the unit. Since we are multiplying these 2 lengths together, the unit for the area will be in the form of square unit.

00:00:42.070
We will see the explanations on this, in the upcoming example.

00:00:47.040
Now, Let’s see some examples on using this formula.

00:00:52.070
Find the area of this square when the length of each side is 3cm.

00:00:58.150
To do so, we start with the formula for the area of a square, A equals to L square.

00:01:05.150
Since the length of each side is 3 cm, we can substitute L with 3.

00:01:11.160
This gives 3 square.

00:01:14.160
Now, let's simplify 3 square.  3 square is actually the same as, 3 multiply by 3, which is 9.

00:01:26.160
Let's write down this number.

00:01:30.030
Now, this number is meaningless unless we include the unit for it.

00:01:35.030
Since the length is given in centimeter, the unit for the area will be in square centimeter.

00:01:41.230
Therefore, the area of this square is 9 square centimeter.

00:01:48.210
Next example, given that the area of this square is 4 square feet, find the length of each side.

00:01:56.190
Now, we start with the formula for the area of a square, A equals to L square.

00:02:03.180
Since the value of the area is given, we can find the length of each side, by solving the equation for L.

00:02:11.060
Here’s how. Since the area is given as 4 square feet, we can substitute A with 4.  

00:02:19.170
Now, we have, L square equals to 4.

00:02:24.020
Let's rewrite this equation so that it will look neater.

00:02:28.150
To find L, we can see that since 4 is equals to L square, L can be found by calculating the square root of 4.

00:02:38.020
Square root of 4 is 2. 

00:02:41.150
Now this number has no meaning unless we include the unit for it.

00:02:47.030
Since the area is given in square feet, the side of the square will be in feet.

00:02:53.170
Therefore, the length of each side of the square is 2 ft.

00:03:00.010
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on the area of a square or pick your choice of question below.

Question 1 on finding the area of a square
Question 2 on finding the length of the sides of a square

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Return to Home Page