Area of a Trapezoid

Lesson Objective

In this lesson, we will learn about the area of a trapezoid.

Study Tips

Tip #1

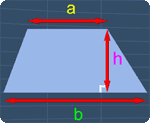
A trapezoid has four sides where two sides are parallel to each other. The height of the trapezoid is perpendicular to the parallel sides. These are shown on the right.

Now, if a trapezoid has the height h and two parallel sides a and b, the area A, of the trapezoid will be:

a trapezoid with the height h and 2 parallel sides, a and b.

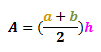
The math video below will give more explanation on this. Also, we will see some examples on how to use this formula.

Math Video

Lesson Video

Sponsored Links

Math Video Transcript

00:00:03.150
In this lesson, we will learn about the area of a trapezoid.

00:00:08.030
First, let's consider this trapezoid with the height ‘h’, and two parallel sides, ‘a’ and ‘b’ respectively.

00:00:17.140
Now, to find the area of a trapezoid A, first we add ‘a' and 'b' together, and divide the added numbers with 2.

00:00:27.010
This gives (a+b)/2. Next, we multiply (a+b)/2, with the height of the trapezoid, ‘h’.

00:00:38.070
Hence, now we have the formula for the area of a trapezoid, A = ((a+b)/2)h.

00:00:47.240
Note that, it is very important to include the unit. Since this is the formula for area, its unit will be in the form of square unit.

00:00:57.020
We will see more explanations on this, in the upcoming example.

00:01:02.040
Now, let's see some examples on using this formula.

00:01:07.030
Find the area of this trapezoid when its height is 4cm, and the parallel sides are 5cm, and 9cm respectively.

00:01:17.080
First, we start with the formula for the area of a trapezoid, A = ((a+b)/2)h.

00:01:26.080
Since the shorter parallel side is given as 5cm, we can substitute ‘a’ with 5.

00:01:33.150
Similarly, since the longer parallel side is given as 9cm, we can substitute 'b' with 9.

00:01:41.230
Next, we can simplify by adding 5 with 9. This gives 14. 

00:01:48.110
14 divided by 2, gives 7.

00:01:52.200
Now, since the height is given as 4cm, we can substitute 'h' with 4.

00:01:59.120
Multiplying 7 with 4, gives 28.

00:02:03.180
Note that, this number has no meaning unless we include the unit for it.

00:02:08.160
Since the sides of the trapezoid are in centimeter, the unit for the area will be in square centimeter.

00:02:15.160
Hence, the area of this trapezoid is 28 square centimeter.

00:02:23.050
Next example, given that the area of this trapezoid is 9 square feet, and it parallel sides are 2ft, and 4ft respectively. Find its height.

00:02:34.200
Again, we start with the formula for the area of a trapezoid, A = ((a+b)/2)h.

00:02:44.040
Now, since the area, and the 2 parallel sides are given, we can find the height by solving this equation for h. Here's how.

00:02:53.240
Since the area is given as 9 square feet, we can substitute 'A' with 9,

00:03:00.100
Similarly, since the shorter parallel side is given as 2cm, we can substitute 'a' with 2.

00:03:08.100
Again, since the longer parallel side is given as 4cm, we can substitute 'b' with 4.

00:03:16.150
We can simplify this equation, by adding 2 with 4. This gives 6. 6 divided by 2, gives 3.

00:03:27.130
(3)h is the same as 3h.

00:03:32.010
Now, we have 3h equals to 9.

00:03:36.140
Let's rewrite this equation so that it will look neater.

00:03:40.190
To find 'h' we need to remove 3. We can do so by dividing both sides of the equation with 3.

00:03:49.040
By doing so, we have, ’h’ equals to 9 over 3.

00:03:54.170
9 divides by 3, gives 3.

00:03:58.190
Now, this number is meaningless unless we include the unit for it.

00:04:03.110
Since the parallel sides are given in feet, the height of the trapezoid will be in feet.

00:04:09.120
Therefore, the height of this trapezoid is 3ft.

00:04:15.010
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on the area of a trapezoid or pick your choice of question below.

Question 1 on finding the area of a trapezoid
Question 2 on finding the height of a trapezoid

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons