Area Word problem: Circles and Leaves

Question

A circular table has an area of 1,256 square inches. The table opens in the middle to allow the additional leaves. Each leaf is 12" wide and is rectangular in shape. How many leaves must be added to change the area of the table to 2,696 square inches?

Answer

STEP 1:    The given question can be approached in a simpler way by just assuming a circle of area 1256 square inches and a rectangle of 12" width, and finding how many additional rectangles is to be added when the area of the circle is 2,696 inches. Let us first find how many more inches are needed for the table to be 2696 inches.

2,696 – 1,256 = 1440 square inches

STEP 2:    So, we have to find the number of rectangles which can be allowed in this 1440 square inches. To proceed further, the measurements to be known are the areas of the circle and the rectangle. It is given that the area of the circle is 1256 square inches. So, the next thing we have to do is to find the area of the rectangle.

To find the area of the rectangle we need to know its length and width. Note that the width of the rectangle is 12" and its length is same as the diameter of the circle. We find the radius of the rectangle first, as we know that the area of the circle is πr² , where r is the radius.
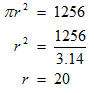
STEP 3:    We now find the diameter of the circle.
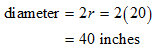
So, the length of the rectangle is 40 inches.

STEP 4:    The area of the rectangle can be easily found now,
as we know both the length and width of the rectangle.
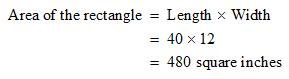
STEP 5:    To find the number of rectangular leaves that can be added to change the area of the circle we just need to divide 1440 by the area of the rectangle.

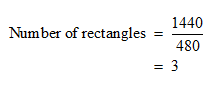
Note that 3 leaves would give an area of 3(480) = 1440 square inches since we found the area of one rectangle as 480 square inches. Also, the area 1440 square inches is exactly what we need to increase 1256 square inches to 2696 square inches.

So, 3 leaves must be added to change the area of the table to 2,696 square inches.