Combining Like Terms

Lesson Objective

This lesson is about identifying and combining like terms in algebraic expressions.

Study Tips

Tip #1

Know how to identify all the terms in the algebraic expression.

Tip #2

'Like terms' are terms that have exactly same variables. Also, the exponent (i.e. power) of the variables must be the same.

Now, watch the following math videos to know more.

Math Video

Video on Combining Like Terms

Sponsored Links

Math Video Transcript

Combining Like Terms

00:00:02.230
The parts of an algebraic expression are called terms. For example, the expression 2 +x +3y has 3 terms. One. Two Three. 

00:00:18.000
You can combine terms that have exactly the same variables. This lesson shows you how. 

00:00:28.060
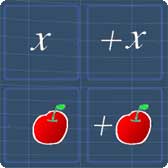
Let's say you're asked to simplify x + x + x. To do so, you must able to recognize which of these  are like terms.  

00:00:38.080
Let's imagine that the variable 'x' is an 'apple' 

00:00:42.180
Hence, 'plus x' becomes 'plus apple'. You see that these apples are the same in type and size. So these apples are considered as alike. 

00:00:53.190
Since these apples are alike, you can add them up to get 3 apples

00:00:58.180
Now, let's change the apple back to x.

00:01:02.190
You can see now that x+x+x gives 3x. Therefore, all the terms in this expression are like terms.

00:01:12.130
Let's take another example on combining like terms,  -x  -x  -x.

00:01:17.220
Again, imagine that the variable 'x' is an 'apple'. Hence, minus x becomes minus apple.

00:01:26.030
Since these apples are alike, you can add them up to get negative 3 apples 

00:01:34.070
Now, let's change the apple back to x.

00:01:38.220
You can see now that  -x -x -x gives -3x

00:01:45.180
Let's take another example on combining like terms,  x + x + y + y 

00:01:51.230
We have a new variable y here. So, let's imagine the variable 'y' is an 'orange'.


00:01:58.220
The each terms in this expression now becomes plus orange, plus apple, plus apple.

00:02:06.000
Now you see that 1 apple plus 1 apple gives two apples. and 1 orange plus 1 orange gives two oranges

00:02:25.050
Let's change these 'apples' back to 'x', you now have  x + x which gives 2x.

00:02:25.050
Let's change these 'oranges' back to 'y',  you now have  y + y which gives 2y.

00:02:36.070
Now, x +x +y +y gives 2x +2y

00:02:42.040
So in summary, you can only add or minus terms that are alike.

00:02:51.050
From the previous examples, you can see that only like terms can be combined

00:02:56.190
Now, let's take a look at more examples on like terms.

00:03:01.090
Both x, and x square, are not like terms.  Why?

00:03:06.220
Imagine that, x is an apple. Then x square must be a bigger apple.

00:03:13.160
Even though, both fruits are apples, the difference in sizes make them not alike.

00:03:19.210
Now, let's take a look at x square, and, x square y power of three. 

00:03:26.080
These are not like terms. To understand this, let's take x square to be a big apple.

00:03:33.050
Then, x square and y power of three will be like some kind if fruit mixture.

00:03:39.040
Now, it is obvious that these fruits are not alike.

00:03:43.240
How about, x square y power of three,  and  two x square  y power of three?


00:03:49.230
These terms are like terms. 

00:03:53.010
To understand this, let  x square y power of three, to be a fruit mixture. 

00:03:58.230
Then,  two x square y power of three, will be 2 times of the same fruit mixture.

00:04:05.150
Now, you see that, the fruits and sizes are the same, and only the number of fruits are different.

00:04:13.010
So, these fruits are alike.

00:04:15.210
That's all for this lesson on combining like terms. Try out the practice questions to strengthen your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on combining like terms or pick your choice of question below.

Question 1 on identifying the number of terms in an expression
Question 2 on identifying like terms in an expression

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons