Dividing Fractions
Lesson Objective
In this lesson, we will use some examples to explain the basics behind dividing fractions.
About This Lesson
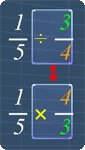
It is quite easy to divide fractions after we have learned to multiply fractions. This is because dividing fractions is closely related to multiplying fractions.
This relation lies in the step needed to convert the division to multiplication. The picture on the right will give you a rough idea on this.
The study tips and math video will explain more.
Study Tips
Tip #1 - Reciprocal of a fraction
We need to know how to find the reciprocal of a fraction before we can proceed. The example below shows how:
-
Find the reciprocal of the following fraction:
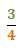
-
To do so, we simply swap the numerator and denominator:

-
Hence, the reciprocal of 3/4 is:
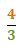
Tip #2 - Dividing Fractions
The following example shows the steps required to divide fractions:
-
First, we change the division to multiplication. Then, we change the divisor 3/4, to its reciprocal, 4/3.
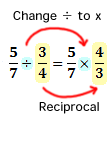
-
After doing so, we can continue by multiplying these fractions:
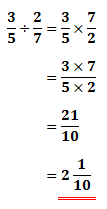
The math video below will give more explanation on this. Also, we will see some examples it.
Math Video
Lesson Video
Sponsored Links

Please support us by downloading our Fraction Basics app and subscribe to get all 12 video lessons and All Access pass to 8 Zapzapmath Home apps with 180 math games from as low as US$1.67/month:
Apple App Store (iOS) |
Google Play (Android)
Math Video Transcript
00:00:02.220
In this lesson, we will learn the basics behind dividing fractions.
00:00:08.090
Let's divide, 1/5 with 3/4.
00:00:13.100
We can do so, by changing this division sign to multiplication sign, provided that we swap the numerator and denominator of the divisor, 3/4, to get its reciprocal, 4/3.
00:00:27.020
To explain this, let's take a look at the division again. Note that, 1/5 divides by 3/4, can be written in the form of fraction, 1/5, over, 3/4.
00:00:42.160
Now, 1/5 is the numerator, and 3/4 is the denominator.
00:00:49.070
Next, let's multiply the denominator with 4/3.
00:00:54.130
To keep this fraction equivalent, we must multiply the numerator with 4/3 as well.
00:01:01.010
Next, notice that these terms cancel off. This is because, 4 divides by 4, and 3 divides by 3 gives 1.
00:01:11.150
Now, we are left with the numerator. Dividing this numerator with 1, gives back itself, 1/5 multiply by 4/3.
00:01:23.060
Here, notice something interesting. By comparing these 2 terms, we observe that this fraction division is the same as fractions multiplication, provided that we change the divisor, 3/4 to its reciprocal, 4/3.
00:01:41.050
Knowing this, let's continue the division by multiplying these fractions.
00:01:47.200
First, multiply the numerators. 1 multiply by 4, gives 4.
00:01:56.050
Next, multiply the denominators. 5 multiply by 3, gives 15.
00:02:05.050
Finally, we have the fraction, 4/15.
00:02:12.220
Next example, let's divide 2/3, with 5/7.
00:02:18.210
We can do so, by changing this division sign to multiplication sign, provided that we swap the numerator and denominator of the divisor, 5/7, to get its reciprocal, 7/5.
00:02:33.080
Now, we can proceed by multiplying these fractions.
00:02:38.120
First, multiply the numerators. 2 multiply by 7, gives 14.
00:02:46.020
Next, multiply the denominators. 3 multiply by 5, gives 15.
00:02:54.060
Finally, we have the fraction, 14/15.
00:03:00.160
This is all for this lesson, try out the practice questions to further your understanding.
--End of Dividing Fractions Transcript--
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on Dividing Fractions or pick your choice of question below.
- Question 1 on how to divide fractions
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


