Equation of a Line Parallel to the X-axis or Y-axis
Lesson Objective
This lesson shows you how to determine the equation of a line that is parallel to the x-axis or y-axis.
About This Lesson
In this lesson, we will learn how to determine the equation of a line that is parallel to the x-axis or y-axis.
This lesson shows you the concepts that you should know about a line that is parallel to the x-axis or y-axis of the coordinate plane. Also, we will see some examples on determining its equation.
You should proceed by reading the study tips and watch the math video below. After that, you can try out the practice questions.
Study Tips
Tip #1
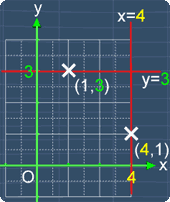
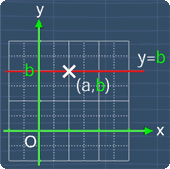
For a line that is parallel to the x-axis, the equation for such a line is:
y = b, where b is some constant
Now, notice that b is the value of the y-coordinate of any point on the line. For example, if b = -2, the equation of the line parallel to the x-axis will be:
y = -2
The math video below will show you the reason behind this.
Tip #2
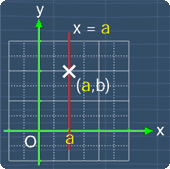
Similarly, for a line that is parallel to the y-axis, the equation for such a line is:
x = a where a is some constant
Also, notice that a is the value of the x-coordinate of any point on the line. For example, if a = 1, the equation of the line parallel to the x-axis will be:
x = 1
The math video below will show you the reason behind this.
Tip #3
Usually, the equation of a line parallel to the x-axis is written this way:
y = 1
For some cases, you may come across the equation above written in this form instead:
y -1 = 0
Now, these two equations are in fact the same, this is because if we add +1 to both sides of the equation, we have:
y -1 +1 = 1
y = 1
So, we can see that there is no difference between these two equations. This explanation also applies to the equation of a line parallel to the y-axis.
Now, watch the following math video to learn more.
Math Video
Lesson Video
Sponsored Links
Math Video Transcript
00:00:01.190
This lesson shows you how to determine the equation of a line, that is parallel to the x-axis or y-axis.
00:00:10.030
Let's consider these 3 points. When we draw, a line through these points, this line will be parallel to the x-axis.
00:00:19.190
Now, notice that all these points have the same y-coordinates of 2.
00:00:25.050
When I move these points up, take note of the values of these y-coordinates.
00:00:30.170
As you can see, the y-coordinates for these points, are always the same as each other.
00:00:37.020
Now, for this case, the y-coordinates for these points is 5.
00:00:42.110
Therefore, from this observation, we can say that every single point on this line, has the y-coordinate of 5.
00:00:50.120
Knowing this, we can simply represent this line with the equation, y = 5.
00:00:58.230
Let's explore further. Take note of the values of these y-coordinates, when I move these points down.
00:01:07.120
Again, notice that the y-coordinates for these points, are the same as each other.
00:01:13.170
Therefore, from this observation, we can say that every single point on this line, has the y-coordinate of -2.
00:01:22.180
Knowing this, we can simply represent this line with the equation, y = -2.
00:01:31.000
Alright, let's consider another 3 points.
00:01:35.110
When we draw a line through these points, we get a line parallel to the y-axis.
00:01:41.040
Now, notice that all these points have the same x-coordinates of 1.
00:01:46.190
When I move these points to the right, take note of the values of these x-coordinates.
00:01:53.070
As you can see, the x-coordinates for these points, are always the same as each other.
00:02:00.040
Therefore, from this observation, we can say that every single point on this line, has the x-coordinate of 2.
00:02:08.170
Knowing this, we can simply represent this line with the equation, x = 2.
00:02:16.210
Let's explore further. Take note of the values of these x-coordinates when I move these points to the left.
00:02:25.170
As you can see, the x-coordinates for these points, are always the same as each other.
00:02:32.160
Therefore, from this observation, we can say that every single point on this line, has the x-coordinate of -4.
00:02:41.150
Knowing this, we can represent this line with the equation, x = -4.
00:02:50.110
Alright, Let's see some examples.
00:02:55.040
Determine the equation of a line, that passes through the point (-3, 4) and is parallel to the x-axis.
00:03:03.220
Now, since the line is parallel to the x-axis, we can draw a horizontal line passing through the point (-3, 4)
00:03:13.070
By observation, since this point have the y-coordinate of 4, this line will have all its points with y-coordinate of 4 as well.
00:03:22.070
Knowing this, we can represent this line with the equation, y = 4.
00:03:29.210
Next, determine the equation of a line, that passes through the point (-3, 4) and is parallel to the y-axis.
00:03:39.160
Now, since the line is parallel to the y-axis, we can draw a vertical line passing through the point (-3, 4)
00:03:49.100
By observation, since this point have the x-coordinate of -3, this line will have all its points with x-coordinate of - 3 as well.
00:03:59.190
Knowing this, we can represent this line with the equation, x = -3.
00:04:06.130
That's all for this lesson. Try out the practice question to test your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions equation of a line parallel to the x-axis or y-axis or pick your choice of question below.
- Question 1 on determining the equation of a line using the coordinates of two points.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


