Determine The Equation of a Line
Lesson Objective
This lesson shows you how to determine the equation of a line by using the given information such as the slope, coordinates of a point, etc.
About This Lesson
In this lesson, we will learn how to determine the equation of a line using the given information.
This lesson will show you two examples on how to do so using the following information:
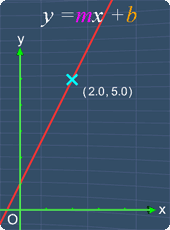
- Point (2,5) and Slope = 2
- Points (1,4) and (2,1)
You should proceed by reading the study tips and watch the math video below. After that, you can try out the practice questions.
Study Tips
Tip #1
You need to have some knowledge on the slope-intercept form of a line. You can learn about it by watching the math video in this lesson.
Tip #2
For the equation of a line that we want to determine, we would usually want that equation to be in the slope-intercept form (see picture).
This way, we just need to use the given information to find the value of the slope (m) and the y-intercept (b).
After doing so, we can easily determine the equation by substituting m and b with their respective value.
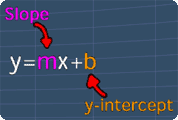
Now, watch the following math video to learn more.
Math Video
Lesson Video
Sponsored Links
Math Video Transcript
Determine the Equation of a Line Transcript
00:00:01.120
In this lesson, we will learn how to determine the equation of a line, using the available information.
00:00:08.040
Let's look at the first example. Determine the equation of the line, that passes through the points (2, 5), and with the slope of 2.
00:00:19.000
To begin, we should know that the equation of a line can be written in the form of y = mx + b, where m is the slope, and b is the y-intercept.
00:00:30.110
From this, to determine the equation of the line, we just need to find the values of m and b.
00:00:37.120
Now, we can see that, the slope m, is already given as 2.
00:00:43.050
Therefore, we can just substitute m with 2, and the equation now becomes y = 2x + b.
00:00:51.070
Next, we need to find the y-intercept, b.
00:00:55.090
Since the value of b is not given, we need to find it.
00:00:59.220
To do so, we know that the line passes through the point 2, 5.
00:01:06.160
Therefore, we can use this point by substituting x with 2, and substituting y with 5.
00:01:13.240
With this, notice that we can now solve for b.
00:01:18.010
To solve for b, multiply 2 with 2. This gives 4.
00:01:23.100
Next, add negative 4 to both sides of the equation. This gives 5 - 4 = b.
00:01:30.240
5 minus 4 gives 1. Hence, we found the y-intercept, b as 1.
00:01:38.190
With this, we can write b as 1.
00:01:44.230
Finally, since we found both m and b, the equation of the line is y = 2x + 1
00:01:54.060
Now, next example.
00:01:56.240
Determine, the equation of the line, that passes through the points (1,4) and (2,1).
00:02:04.190
Again, we should know that the equation of a line can be written in the form of y = mx + b.
00:02:12.060
We can see that, the slope and y-intercept are not given. Instead, we only have the coordinates of 2 points.
00:02:20.210
With some thinking, we can use these 2 points to find the slope 'm' by applying the slope formula, (y2-y1)/(x2-x1).
00:02:32.140
To use the slope-formula, we can assign this point as point 1, with the x-coordinate as x1, and y-coordinate as y1.
00:02:42.000
Similarly, we assign the next point as point 2, with x-coordinate as x2, and y-coordinate as y2.
00:02:50.230
Now, we can find 'm' by just substituting, y2 with 1, y1 with 4, x2 with 2, and x1 with 1.
00:03:04.100
Alright, we can remove these brackets, as they do nothing.
00:03:09.220
Let's calculate 'm'. Negative multiply by bracket 4 gives negative 4. negative multiply by bracket 1 gives negative 1.
00:03:20.150
1 minus by 4 give negative 3. 2 minus by 1 gives positive 1.
00:03:27.230
Negative 3 divides by positive 1 gives negative 3.
00:03:32.140
So, we found the slope 'm' as negative 3. Now, we can write m as negative 3.
00:03:42.120
Next, we need to find the y-intercept, b.
00:03:48.080
Now, similar to the previous question, we can find b by taking a point on the line, and substitute its x-coordinate and y-coordinate into the equation.
00:03:59.000
Let's take this point 1,4.
00:04:02.200
Substituting x with 1 and y with 4.
00:04:07.220
Now, we can solve for 'b'. Multiplying negative 3 with 1 gives negative 3.
00:04:14.000
Next, add positive 3 to both sides of the equation. This gives 4 + 3 = b.
00:04:21.120
4 plus 3 gives 7. Hence, we find the y-intercept, b is 7.
00:04:29.010
With this, we can now write b as 7.
00:04:34.120
So finally, with both slope and y-intercept found, we have the equation of the line as, y = negative 3x + 7
00:04:44.060
That is all for this lesson. Try out the practice question to further your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on determining an equation of a line parallel to the x-axis or y-axis or pick your choice of question below.
- Question 1 on determining the equation of a line using the coordinates of two points.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


