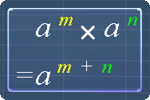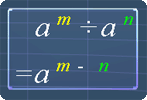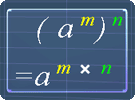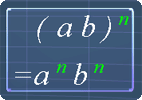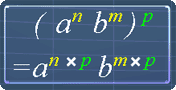Math Expression: Exponent Laws Questions

Simplify the following expression:

The following pictures are the exponent laws. You can use them as reference.

Step 1

Let's first focus on the numerator:

6(q²s³)²

Using the exponent law* as shown in the picture, we get:

6(q²s³)² = 6q^{2 x 2} s^{3 x 2}

*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
Step 2

Now,

2 multiply by 2 gives 4, and
3 multiply by 2 gives 6.

Hence, we have 6q⁴s⁶.
Step 3

Next, let's focus on the denominator:

2(qs²)³

Using the exponent law* as shown in the picture, we get:

2(qs²)³ = 2q^{1 x 3} s^{2 x 3}

*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
Step 4

Now,

1 multiply by 3 gives 3, and
2 multiply by 3 gives 6.

Hence, we have 2q³s⁶.
Step 5

Now, after simplifying the numerator and denominator, the original expression becomes:

6q⁴s⁶ ÷ 2q³s⁶
Step 6

Using the exponent law as shown in the picture, we get:

6q⁴s⁶ ÷ 2q³s⁶
= 3q^{4 - 3} s^{6 - 6}
Step 7

Simplifying,

3q^{4 - 3} s^{6 - 6}

We get:

3q¹ s⁰

Now, we can write:

q1 as q and,
s0 as 1
Step 8

Finally, we have the simplest term, 3q

Clearly, the answer is C.