Find the equation of the line as described below

Question

Find the equation of the line passing through (–4, 6) and parallel to the line y = 3x + 8.

Answer

STEP 1:    You are given the equation of a line to be used it to find the equation of another line which is parallel to this line, and passing through the point (–4, 6).

Remember that parallel lines have the same slope. This gives us a clue that we have to start working by finding the slope of the given line. Since the equation is already in the slope-intercept form (y = mx + b), you can easily find the slope.

Make a note of what each variable in the equation stands for:Compare with the standard form.
The slope of the given line is 3, and so it is the slope of the parallel line
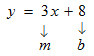
also.

Use 3 for m in the equation:STEP 2:    The value of b is still unknown. Since the line is said to pass through (–4, 6), you can substitute the respective values for x and y.
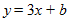
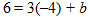
Now, solve the equation for b.
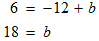
STEP 3:   The final step is to replace all the variables in the slope-intercept form with the known values.
The equation of the line satisfying the given conditions is
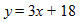
y = 3x + 18.