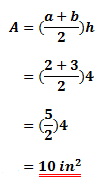Formula for Area
Introduction
This page contains the formula for area of a:
Examples are given to show you how to use the formulas.
Square
Formula
The lesson on the area of a square will explain the basics needed to understand this formula. Here's the summary:
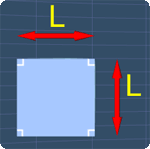
All the sides (edges) of a square have the same length. If each side has the length L, the formula for the area A will be:
Example
Given a square where the length of each side (edge) is 5cm. Find the area of this square.
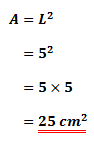
Rectangular Solid
Formula
The lesson on the area of a rectangle will cover the basics needed to use this formula. Here's a short summary:
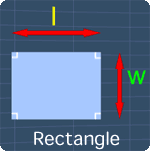
If a rectangle has the length l and the width w, we can find the area A, by multiplying its width and its length together. Hence, we have:
Example
Given a rectangle with the length of 4ft and the width of 3ft. Find its area.
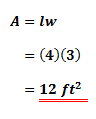
Circle
Formula
The lesson on the area of a circle will explain to you on how to use this formula. Here's a short summary:
For a circle with the radius r, its area A, will be:
Where π is constant that is approximately equals to 3.14.

Example
Given a circle with the radius 3cm. Find its area. Take π = 3.14.
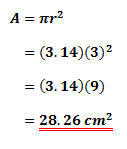
Parallelogram
Formula
The lesson on the area of a parallelogram will show you the basic ideas on using this formula. Here's a summary:
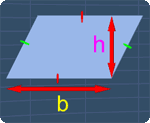
For a parallelogram with the base b and the height h, the area A, is given as:
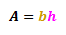
Example
Given a parallelogram with the base 5in and the height 3in. Find the area of this parallelogram.
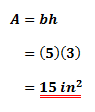
Triangle
Formula
The lesson on the area of a triangle will explain to you on how to use this formula.
Consider a triangle with the base b and height h, the area A, of this triangle is simply:
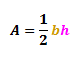
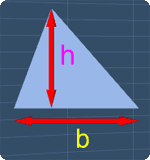
Example
Given a triangle with the base 4cm and the height 2cm. Find its area.
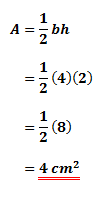
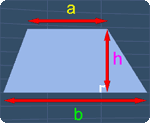
Trapezoid (Trapezium)
Formula
The lesson on the area of a trapezoid will explain the steps on using its formula for area. Here's the summary:
For a trapezoid with the height h and two parallel sides a and b, its area A, is given as:
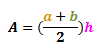
Example
Given a trapezoid with the height of 4in, and two parallel sides of 2in and 3in respectively. Calculate its area.