Slope-Intercept Form Examples

Lesson Objective

After learning about the slope-intercept form, let's see some examples on using it to draw the line for any equation of a line (linear equation).

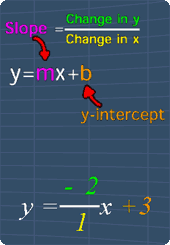
Study Tips

Tip #1

This lesson involves some knowledge on slope-intercept form of a line. You can learn about it by watching the math video in this lesson.

Tip #2

If you are given an equation of a line, it may not be in the slope-intercept form.

Therefore, it is important to change it into the slope-intercept form (see picture) before we can draw the line. For example, if the equation of the line is given as:

                   2y - 6x = -4

The slope-intercept form for this line will be:

                    y = 3x -2

Where m = 3 and y-intercept = -2

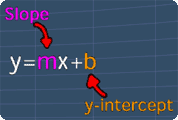
Now, watch the following math video to learn more.

Math Video

Click play to watch video

Sponsored Links

Math Video Transcript

00:00:01.130
This lesson shows you some examples on how to draw the graph of the equation of a line, that is in the form of slope-intercept.

00:00:09.180
Let's consider the equation, y = -2x + 3.

00:00:15.100
Now, we can see that this equation is already in the slope-intercept form, with the slope as  -2, and the y-intercept as +3.

00:00:25.040
So, how do we use the slope and the y-intercept to draw the line?

00:00:30.220
To draw the line, we use the y-intercept first. Since the y-intercept is +3, we know the line will cross the y-axis at  +3.

00:00:41.100
Therefore, we can put a point with the coordinates of (0,3) here.

00:00:47.050
Next, with the slope of the line as -2, we can use this information, if we know that the slope is equals to 'change in y' over 'change in x'.

00:00:57.190
Since the 'change in y' over 'change in x' is a fraction, we need to change -2 into a fraction so it can be used.

00:01:06.200
To do so, we simply rewrite -2 as, -2 divides by 1. Since this division gives back  -2, the slope remains the same.

00:01:18.190
With this, we now know that the 'change in y' is -2, and the 'change in x' is 1.

00:01:26.130
Now, to use, 'change in y' and 'change in x' , we need to refer these 'change' from a point on the line.

00:01:34.240
Now, the only point that we can refer from, is the point (0,3).

00:01:41.170
So, starting from here, since the 'change in y' is -2, we move down from this point by 2 units.

00:01:50.010
Next, since the 'change in x' is +1, we move from here to the right by 1 unit.

00:01:57.190
Notice that now we have 2 points. By drawing a line through these points, we have the graph of y =-2x + 3.

00:02:07.230
Next example, let's draw the graph of 3y -2x =  -6.

00:02:15.000
Now, Notice that we have a problem, this is because the given equation is not in the form of y = m x + b. 

00:02:22.120
Hence, we need to manipulate this equation into this form before we can draw it.

00:02:28.000
To do so, we need to make 'y' as the subject of the equation. So, in order to achieve this, we need to remove -2x.

00:02:37.220
We can do so by adding +2x to both sides of the equation.  

00:02:42.210
This give 3y = +2x -6. Now, we can remove this positive sign to make the equation looks neater.

00:02:52.200
Next, we need to remove '3' from 3y. To do so, we divide both sides of the equation by 3.

00:03:00.210
By dividing both sides by 3, we get the equation as y = 2x -6 divide by 3.

00:03:08.040
Now, we can split this term into 2 fractions. This gives y = 2x/3 -6/3.

00:03:17.130
6 divides by 3 gives 2.  

00:03:20.210
2x divides by 3 can also be written in this way. Finally, you can see that we have change the equation into the form of y = mx + b.

00:03:32.100
Now, clearly the y-intercept is -2. Hence, the line will cross the y-axis at -2. 

00:03:40.050
Therefore, we can put a point with the coordinates of (0,-2) here.

00:03:45.180
Next, we know that  2/3 is the slope with the 'change in y' of 2 and the 'change in x' of 3.

00:03:55.040
Now, to use, 'change in y' and 'change in x', we need to refer these 'change' from a point on the line. 

00:04:03.220
The only point that we can refer from, is the point (0, -2)

00:04:09.140
So, starting from here, since the 'change in y' is +2, we move up from this point by 2 units.

00:04:17.200
Next, since the 'change in x' is +3, we move from here to the right by 3 units.

00:04:25.130
Notice that now we have 2 points. By drawing a line through these points, we have the graph of 3y -2x =  -6.

00:04:36.200
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on slope-intercept or pick your choice of question below.

Question 1 on the changing an equation of a line into
slope-intercept form
Question 2 on drawing a line by referring to the slope and
y-intercept of a line

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons