Using a Protractor (Measuring Angles)
Lesson Objective
In this lesson, we will learn how to measure angles using a protractor.
About This Lesson
In this lesson, we will:
- Learn what is a protractor. The following picture shows the parts of a protractor.
- Learn how to use a protractor to measure angles that are:
- Less than 180° (1st math video)
- Greater than 180° (2nd math video)
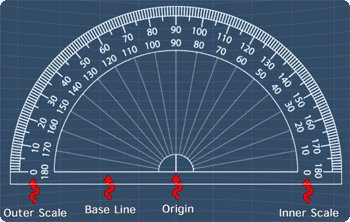
The study tips and math video below will explain more.
Study Tips
Tip #1
It is important to ensure the following when using a protractor:
- The protractor's origin is at the vertex of an angle.
- The protractor's base line is along the arm.
- Make sure that you are using the appropriate scale when reading the angle. For example, the angle below is 50° and not 130°:
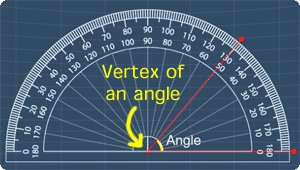
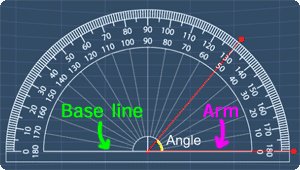
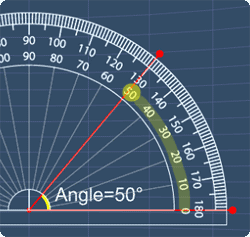
The math videos below will explain more on this.
Math Video
Video on parts of a protractor & measuring angles that are <180°
Sponsored Links

Get to know angles better in a fun interactive way by downloading our free Zapzapmath Home Grade 4 and playing Angle Align:
Apple App Store (iOS) |
Google Play (Android)
Math Video Transcript
00:00:04.070
In this lesson, we will learn how to use a protractor to measure angles.
00:00:10.220
Now, this is a protractor. The point here is the 'origin'. This is the base line, the inner scale the outer scale.
00:00:33.060
Knowing this, let's use this protractor to measure angles.
00:00:38.070
Measure this angle, ABC. First, we place the protractor's origin, on the vertex B.
00:00:48.150
Next, make sure that the base line is along the line BC.
00:00:54.120
Looking at the inner scale, we can see that this angle is 70 degrees.
00:01:01.000
Hence, the angle ABC is equals to 70 degrees.
00:01:08.170
Next example, find the value of this angle, ABC.
00:01:14.130
To do so, we place the protractor's origin, on the vertex B.
00:01:20.190
Next, make sure that the base line is along the line BC.
00:01:27.100
Now, from the inner scale, the angle is measured as, 51, 52, 53, 54, 55 degrees.
00:01:32.140
Hence, the angle ABC is equals to, 55 degrees.
00:01:42.220
Next example, measure the angle, ABC.
00:01:50.190
Similarly, we place the protractor's origin on the vertex B, and make sure the base line is along the line, BC.
00:01:55.110
From the inner scale, we can see that, this angle is 130, 131, 132 degrees.
00:02:17.050
Hence, the angle ABC is equals to 132 degrees.
00:02:17.070
That is all for now.
Video on measuring angles that are >180° using a protractor
| |
Math Video Transcript
00:00:04.000
In this lesson, we will learn on using a protractor to measure any angle that is greater than 180 degrees.
00:00:12.08
Now, measure this angle, ABC.
00:00:16.070
To measure this angle, we split this angle into 2 parts, by drawing a dotted line along BC.
00:00:24.050
By finding the sum of these 2 angles, we will get the angle ABC.
00:00:29.120
Now, we place the protractor, at the vertex B.
00:00:34.170
Next, we rotate the protractor to that its base line is along BC.
00:00:41.130
Here, we can see that, this angle is 180 degrees.
00:00:50.050
Next, to measure this angle, we rotate the protractor, so that its baseline is along the line AB.
00:00:59.040
From the outer scale, we can see that, this angle is 40 degrees.
00:01:08.080
Hence, the angle ABC is equals to 180 degrees, plus 40 degrees.
00:01:15.180
This gives 220 degrees. Therefore, the angle ABC is 220 degrees.
00:01:26.130
Next example, measure this angle x using a protractor
00:01:31.170
By now, we should know that the angle for a full rotation is 360 degrees.
00:01:38.150
Therefore, we can find x, by taking 360 degrees, minus this angle.
00:01:46.220
So, let’s measure this angle using a protractor.
00:01:51.220
To do so, we place the protractor's origin, here.
00:01:56.230
Then, make sure that the base line is along this line.
00:02:03.060
From the outer scale, we can see that this angle is 60, 61, 62, 63, 64, 65 degrees.
00:02:24.000
Hence, x is equals to, 360 degrees, minus by 65 degrees. This gives 295 degrees.
00:02:36.080
That is all for this lesson, try out the practice question to further your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on using a protractor or pick your choice of question below.
- Question 1 on measuring an angle that is lesser than 180°
- Question 2 on measuring an angle that is greater than 180°
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


